עומק שדה

כולנו יודעים שצמצם פתוח מקטין את עומק השדה וצמצם סגור מגדיל אותו. אבל מה זה בדיוק עומק שדה, למה הוא מושפע מהצמצם, איך הוא מושפע מאורך המוקד של העדשה ואיך אפשר למקסם אותו כדי להגדיל ככל האפשר את האזור בתמונה שיהיה בפוקוס?
מסתבר שכל השאלות האלו קשורות. כל התשובות בהמשך.

אורך מוקד של עדשה

עדשות מצלמה בנויות ממספר רב של אלמנטים אופטיים, שכל אחד מהם הוא עדשה ששוברת את קרני האור בנפרד. התייחסות לכל האלמנטים האלו היא גם מסובכת וגם תלויה במבנה הספציפי של כל עדשה, לכן, כדי לפשט את הדיון, נניח שמדבור בעדשה דקה, שנמצאת במרכז האפקטיבי של העדשה הגדולה. למי שזוכר פיזיקה תיכונית, הדבר דומה להתייחסות למרכז המסה של גוף כנקודה במקום למבנה התלת מימדי המלא שלו.

אורך המוקד (focal length) של עדשה קמורה (f) מוגדר כמרחק בין המרכז האפקטיבי של העדשה לנקודה שבה אור שמגיע מאינסוף יתמקד:

מקדם הגדלה

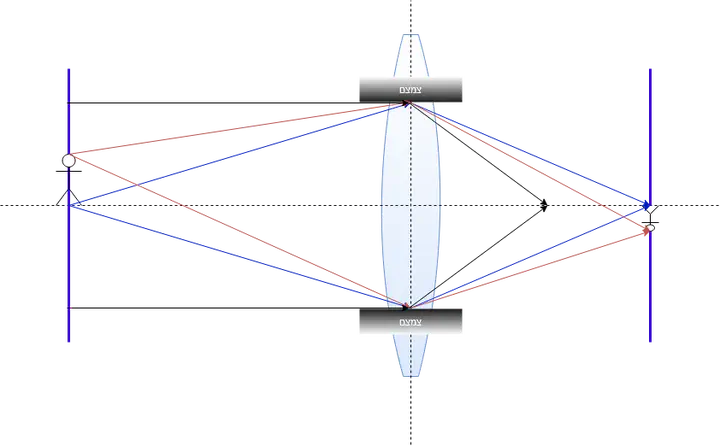
נסתכל על שרטוט סכמתי של אובייקט שעומד מול עדשה והתמונה שלו מוקרנת על מסך:

המישור בו ממוקם האובייקט המצולם נקרא מישור האוביקט ונסמן את המרחק אליו באות u.
המישור בו יעמוד המסך, באופן כזה שתיווצר עליו תמונה חדה/ממוקדת, יקרא מישור התמונה ונסמן את המרחק אליו באות v.

מקדם ההגדלה של העדשה (m) מוגדר ע"י היחס בין המרחק v למרחק u : $$\tag{1} m=\frac{v}{u} $$

הנוסחה הזו מייצגת את העובדה הפשוטה שכולנו מכירים, עבור עדשת מצלמה עם אורך מוקד כלשהו המרחק v הוא נתון כיוון שהמיקום של החיישן (המסך עליו מוקרנת התמונה) הוא קבוע. ככל שנתרחק מהאובייקט u יגדל ולכן m יקטן והאובייקט יראה קטן יותר ולהפך, ככל שנתקרב u יקטן, m יגדל והאובייקט יראה גדול יותר.

הקשר בין אורך המוקד של העדשה למישורי האובייקט והתמונה

הנוסחה הבאה מציגה את הקשר בין שלושת המרחקים שדיברנו עליהם עד כה: $$\tag{2} \frac{1}{f} = \frac{1}{v} + \frac{1}{u} $$ ועם קצת מניפולציה נקבל: $$\tag{3} f = \frac{vu}{v+u}$$ $$\tag{4} v = \frac{uf}{u-f}$$ $$\tag{5} u = \frac{vf}{v-f}$$

מכאן אפשר להסיק שתי מסקנות מעניינות:

• כאשר האובייקט מאוד רחוק (“באינסוף”) $u \to \infty $ מתקבל ש- $\frac{1}{u} \to 0$ ולכן $ f = v$ שזו בדיוק ההגדרה של אורך המוקד של העדשה כפי שניתנה קודם.
  או במילים פשוטות, כאשר מתמקדים על אינסוף מישור התמונה הוא בדיוק אורך המוקד של העדשה.

• עבור עדשה נתונה בעלת אורך מוקד f כלשהו, אפשר לראות שיש קשר הפוך בין u ל-v, כלומר כאשר u גדל v חייב לקטון ולהפך. ובמילים אחרות, מרחק מישור התמונה יהיה שונה עבור כל מרחק אובייקט.
  אם נשתמש בנוסחה (4) כדי לחשב את מרחק מישור התמונה עבור עדשת 50מ"מ ובנוסחה (3) כדי לקבל את אורך המוקד הנדרש כדי למקד אובייקטים שונים על מישור תמונה במרחק 50 מ"מ נקבל:

  מרחק אובייקט	מרחק מישור התמונה עבור עדשה עם אורך מוקד 50 מ"מ	אורך המוקד הנדרש אם מישור התמונה נמצא במרחק 50 מ"מ
  אינסוף	50 מ"מ	50 מ"מ
  10 מ'	50.25 מ"מ	49.75 מ"מ
  3 מ'	50.84 מ"מ	49.18 מ"מ
  1 מ'	52.63 מ"מ	47.61 מ"מ
  25 ס"מ	62.50 מ"מ	38.46 מ"מ

  
  
  ה"מסך" במצלמה הוא החיישן אבל מקומו בגוף המצלמה הוא קבוע ולא ניתן להזזה, יוצא מכך שלכל אורך מוקד יש בדיוק מרחק אובייקט אחד שיהיה בפוקוס מושלם!

איך עדשות מתמקדות

לאור הקביעה הקודמת מתבקשת השאלה איך עדשות עם אורך מוקד קבוע (עדשות פריים), בכל זאת מצליחות להתמקד במרחקים שונים, הרי הרגע אמרנו שזה בלתי אפשרי? התשובה היא, שגם בעדשות פריים אורך המוקד לא לגמרי קבוע. בתהליך המיקוד (הפוקוס) זזים אלמנטים בתוך העדשה באופן שמשנה את אורך המוקד האפקטיבי שלה. יש עדשות שבהן אפשר אפילו לראות זאת אם מסתכלים לתוך העדשה תוך כדי שינוי הפוקוס. כלומר, גם עדשת פריים, שלכאורה אורך המוקד שלה קבוע, חייבת לשנות אותו כדי להתמקד על אובייקטים במרחקים שונים.
ה"מזל" הוא שכיוון שאורך המוקד והמרחק של מישור התמונה v קטנים מאוד ביחס ביחס למרחק מהאובייקט u מספיק שינוי קטן באורך המוקד כדי לפצות על שינוי גדול במרחק של האובייקט. ככל שהיחס הזה מתקצר נדרש שינוי גדול יותר באורך המוקד כדי לשמור על פוקוס, כפי שניתן לראות בטבלה שלמעלה. לכן כל העדשות מגבילות את מרחק המיקוד המינימלי שלהן כך שלא יצטרכו לשנות את אורך המוקד יותר ממה שסביר מבחינה מכנית.

מה זה עומק שדה

כבר ראינו שעבור כל אורך מוקד יש בדיוק מרחק אובייקט אחד שנמצא במיקוד מושלם, לכן עומק השדה מתייחס לאזורים שנמצאים לפני ואחרי מישור האובייקט ואשר ייצרו תמונה חדה מספיק במישור התמונה למרות שאינם בפוקוס מושלם במישור זה.

התשובה לשאלה מתי תמונה “חדה מספיק” מוגדרת ע"י מושג בעל השם המשעשע באנגלית “מעגל הבילבול” (CoC - Circle of Confusion) אבל כדי למנוע בילבול אני אקרא לו מעגל הטעות.
מעגל הטעות הוא הגבול שמתחתיו גם נקודה ש"נמרחה" ואינה בפוקוס מושלם על מישור התמונה עדיין תיראה חדה לעין אנושית תחת תנאי צפיה מסויימים, ויש מספר גורמים שמשפיעים עליו:

• רזולוציית התמונה - ככל שרמת ההבחנה בין פרטים בתמונה הניצפית, בין אם היא מודפסת או על מסך, גבוהה יותר כך מעגל הטעות יהיה קטן יותר.
• מרחק הצפיה - ככל שמרחק הצפיה יגדל (עבור אותו גודל של הדפסה/מסך) מעגל הבלבול יגדל גם הוא.
• מידת ההגדלה - היחס בין גודל הסנסור לתמונה הניצפית, בין אם היא מודפסת או ניצפית על מסך, ככל שהיחס גבוה יותר, כלומר התמונה הניצפית גדולה יותר כך מעגל הטעות יקטן.
• גודל הפיקסלים בחיישן - מריחה הקטנה משיטחו של פיקסל בודד לא ניתנת להבחנה ולכן ככל שהגודל הפיזי של הפיקסלים גדול כך מעגל הטעות יגדל. גורם זה לא רלוונטי בצילום בפילם.

ערכים קלאסיים של CoC מבוססים רק על שלושת הגורמים הראשונים ובדרך כלל מניחים רזולוציית תמונה של 5 קווים למ"מ ומרחק צפיה של 25 ס"מ. מכאן נובע כלל אצבע עבור מצלמות Full Frame שמעריך את מעגל הטעות ב-$\frac{d}{1500}$ כאשר d הוא אורך אלכסון התמונה הניצפית במ"מ.

לצורך הדיון שלנו, הערכים של CoC לא ממש חשובים אלא עצם העיקרון: כל עוד קוטר ה"מריחה" קטן מקוטר מעגל הטעות גם נקודה מרוחה תיראה חדה.

בדיאגרמה הבאה מופיע אובייקט שנמצא במרחק u מהעדשה ומישור התמונה שלו נמצא במרחק v ממנה. כל נקודה שנמצאת במרחב האובייקט בין $u$ ל-$u_n$ ובין $u$ ל-$u_f$ תייצר עיגול על מישור האובייקט במקום נקודה אבל כל עוד קוטר העיגול הזה קטן מקוטר מעגל הטעות (המסומן ב-c) הנקודות האלו יראו חדות בתמונה הסופית. לכן עומק השדה הוא כל האזור המסומן בצהוב.

נחשב את עומק השדה

👈זהירות נמר - לא ללחוץ👉

כל הכבוד, אתם לא מפחדים מנמרים. מה לגבי קצת מתמטיקה?
נזכיר שבשרטוט הקודם מישור האובייקט נמצא במרחק u מהעדשה ומישור התמונה שלו נמצא במרחק v ממנה. המרחקים $u_n$ ו-$u_f$ מסמנים את הנקודה הקרובה ביותר והרחוקה ביותר, בהתאמה, שעדיין יהיו חדות מספיק במישור התמונה. המרחק למישורי התמונה המתאימים לנקודות אלו יסומן ע"י $v_n$ ו-$v_f$ בהתאמה. מעגל הטעות יסומן ע"י c, קוטר פתח הצמצם ע"י D ואורך המוקד של העדשה ע"י f.
עכשיו ננסה לחשב את המרחקים $u_n$ ו-$u_f$ בהנחה שידועים המרחק לאובייקט, אורך המוקד של העדשה, מספר הצמצם וקוטר מעגל הטעות.

נתחיל בבחינה של שני המשולשים הצבועים בירוק ובכתום בשרטוט הבא:

המשולשים האלו הם משולשים דומים (זה הזמן להזכר בדמיון משולשים מבית הספר) ולכן היחסים בין הניצבים של המשולש הם זהים ומתקיים: $$\frac{\frac{D}{2}}{v_n} = \frac{\frac{c}{2}}{v_n-v}$$ ואחרי היפוך צדדים וצמצום מתקבל: $$\tag{6} \frac{v_n-v}{v_n} = \frac{c}{D} $$

עכשיו נסתכל על שני המשולשים המסומנים בשרטוט הבא:

גם שני משולשים אלו דומים ולכן מתקיים: $$\tag{7} \frac{v-v_f}{v_f} = \frac{c}{D} $$

עכשיו ניזכר שהנוסחה לחישוב f-number היא $N=\frac{f}{D} $
כיוון שבתחילת המאמר הנחנו שאנחנו עוסקים בעדשה דקה, כלומר אין אלמנטים אופטיים נוספים לפני הצמצם, אישון הכניסה יהיה זהה לחריר הצמצם ונוכל להניח ש-D הוא פשוט קוטרו של החריר. אחרי היפוך קטן מתקבל: $D=\frac{f}{N}$

נוכל להחליף את D בנוסחאה (6) עם הערך הזה ונקבל: $$\frac{v_n-v}{v_n} = \frac{c}{\frac{f}{N}} = \frac{Nc}{f}$$

נחלץ את $v_n$ ונקבל:
$$\tag{8} v_n = \frac{fv}{f-Nc} $$

נעשה את אותו דבר לנוסחה (7) ונקבל: $$\tag{9} v_f = \frac{fv}{f+Nc} $$

עכשיו נשתמש בנוסחה (3) כדי להחליף את v בנוסחאות (8) ו-(9) ונקבל בהתאמה: $$\tag{10} v_n = \frac{f\frac{uf}{u-f}}{f-Nc} = \frac{uf^2}{uf-f^2+Nc(f+u)} $$ $$\tag{11} v_f = \frac{f\frac{uf}{u-f}}{f+Nc} = \frac{uf^2}{uf-f^2+Nc(u-f)} $$

כלומר, הצלחנו לבטא את $v_n$ ו-$v_f$ בעזרת המרחק ממישור האובייקט. כל שנותר עכשיו הוא להציב את $v_n$ ו-$v_f$ שקיבלנו לתוך נוסחה (5) כדי למצוא את $u_n$ ו-$u_f$.

בעזרת המשוואות האלו נוכל לחשב את גודלו של עומק השדה מתחילתו עד סופו פשוט ע"י $v_f-v_n$.
מהתבוננות קצת יותר מעמיקה במשוואות ניתן ללמוד מספר דברים מעניינים:

מרחק היפרפוקאלי - Hyperfocal Distance

המרחק ההיפרפוקלי הוא המרחק למישור האובייקט שבו עומק השדה יהיה מקסימלי. כיוון שעומק השדה מאחורי מישור האובייקט תמיד יהיה גדול יותר מעומק השדה לפניו כדי למצוא את עומק השדה המקסימלי נחפש את המרחק הקרוב ביותר שבו עומק השדה שמאחורי האובייקט יהיה אינסוף.
כיוון שאנחנו מחפשים מרחק אובייקט שבו הקצה הרחוק של עומק השדה יהיה באינסוף נתחיל בחילוץ של u מתוך משוואה (11) ונקבל: $$\tag{14} \frac{u_f f^2}{f^2+u_fNc}+f $$ וכאשר $u_f$ שואף לאינסוף נקבל: $$\tag{15} u_h = \lim_{u_f \to \infty} \frac{u_f f^2}{f^2+u_fNc}+f = \frac{f2}{Nc}+f$$ בעזרת הצבה לנוסחה (10) נוכל לחשב את הקצה החקרוב של עומק השדה כאשר מישור האובייקט נמצא במרחק ההיפרפוקלי ונקבל כי: $$\tag{16} u_{h_n} = \frac{u_h}{2} $$

כשעומק השדה אינו מספיק

צלמי נוף נתקלים לעיתים במצבים בהם גם השימוש במרחק היפרפוקלי אינו מספיק כדי שגם האזורים הקרובים לצמלמה יהיו בפוקוס. כזכור כל מה שקרוב יותר ממחצית המרחק ההיפרפוקלי לא יהיה חד בתמונה הסופית. במצב זה ניתן להשתמש בטכניקה שנקראת הערמת פוקוס (Focus Stacking). בשיטה זה יש לצלם תמונה אחת במרחק ההיפרפוקלי ואז לצלם תמונות נוספות, שיתמקדו באזורים הקרובים יותר למצלמה. חלק מהאפליקציות שמחשבות עומק שדה יודעות לעבוד גם במצב של הערמת פוקוס ולהמליץ בדיוק כמה תמונות לצלם ובאיזה מרחקי מוקד כדי לכסות את כל הסצנה הרצויה.
בשלב העריכה יש לפתוח את כל התמונות כשכבות בפוטושופ, לבחור את כולן ואז לבחור בתפריט Edit→Auto-Blend Layers. בחלונית שתופיע יש לבחור Blend Method: Stack Images. פוטושופ תייצר, באופן אוטומטי, mask על כל שכבה כך שהאזור החד ביותר מכל אחת מהתמונות יבחר וימוזג לתמונה הסופית.